Pyslvs API

Module pyslvs

Kernel of Pyslvs.

all_collections()

Full name: pyslvs.all_collections

return
collections.abc.Iterator[str]

Get all collection names.

all_examples()

Full name: pyslvs.all_examples

return
collections.abc.Iterator[str]

Get all example names.

class Collection

Full name: pyslvs.Collection

Bases
TypedDict

Members	Type
cus	dict[int, int]
expression	str
graph	collections.abc.Sequence[tuple[int, int]]
input	collections.abc.Sequence[tuple[Tuple[int, int], Sequence[float]]]
placement	dict[int, Tuple[float, float, float] | None]
same	dict[int, int]
target	dict[int, Sequence[Tuple[float, float]] | None]

collection_list()

Full name: pyslvs.collection_list

key	return
str	Collection

The example data of collections.

The format of each configuration is:

• expression: Mechanism expression of the structure.
  • type: str
• input: Input pairs.
  • type: Sequence[Tuple[int, int]]
• graph: The generalized chain graph in edge set.
  • type: Sequence[Tuple[int, int]]
• placement: The grounded joints setting. (x, y, r)
  • type: Dict[int, Optional[Tuple[float, float, float]]]
• target: The target joints settings.
  • type: Dict[int, Optional[Sequence[Tuple[float, float]]]]
• cus: The custom joints on specific link. (link number correspond to the graph expression.)
  • type: Dict[int, int]
• same: The multiple joints setting.
  • type: Dict[int, int]

color_rgb()

Full name: pyslvs.color_rgb

name	return
str	tuple[int, int, int]

Get color by name.

Get RGB color data by name, return (0, 0, 0) if it is invalid. Also support "(R, G, B)" string format.

class Coord

Full name: pyslvs.Coord

Members	Type
x	float
y	float

A data class used to store coordinates.

Coord.__init__()

Full name: pyslvs.Coord.__init__

self	x	y	return
Self	float	float	Any

Initialize self. See help(type(self)) for accurate signature.

Coord.distance()

Full name: pyslvs.Coord.distance

self	p	return
Self	Coord	float

Return the distance between two coordinates.

Coord.is_nan()

Full name: pyslvs.Coord.is_nan

self	return
Self	bool

Return true if the coordinate value is not a number.

Coord.slope_angle()

Full name: pyslvs.Coord.slope_angle

self	p	return
Self	Coord	float

Slope angle of two coordinates.

edges_view()

Full name: pyslvs.edges_view

graph	return
pyslvs.expression_parser.graph.Graph	collections.abc.Iterator[tuple[int, Tuple[int, int]]]

The iterator will yield the sorted edges from graph.

efd_fitting()

Full name: pyslvs.efd_fitting

path	n	harmonic	return
collections.abc.Sequence[Tuple[float, float]] | numpy.ndarray	int	int | None	numpy.ndarray
	0	None

Curve fitting using Elliptical Fourier Descriptor.

The path path will be translated to Fourier descriptor coefficients, then regenerate a new path as a n x 4 NumPy array.

class EStack

Full name: pyslvs.EStack

Members	Type
well_done	bool

Triangle solution stack, generated from t_config. It is pointless to call the constructor.

EStack.as_list()

Full name: pyslvs.EStack.as_list

self	return
Self	list[tuple[str, ...]]

Copy the dataset as list object.

example_list()

Full name: pyslvs.example_list

key	return
str	tuple[str, collections.abc.Sequence[Tuple[int, int]]]

The example data of mechanisms.

The format of each mechanism is:

• [0]: Mechanism expression.
  • type: str
• [1]: Input pairs.
  • type: Tuple[Tuple[int, int], …]]

expr_solving()

Full name: pyslvs.expr_solving

exprs	vpoints	angles	return
pyslvs.tinycadlib.topo_config.EStack	collections.abc.Sequence[pyslvs.tinycadlib.expression.VPoint]	collections.abc.Mapping[Tuple[int, int], float] | None	list[_Coord | Tuple[_Coord, _Coord]]
		None

Solver function of Triangular method and BFGS method, for mechanism expression vpoints.

The triangle expression stack expr is generated from t_config.

Solver function will not handle slider input pairs in argument angles, which is only support revolute joints. In another way, the slider input pairs can be set by VPoint.disable_offset() method.

get_include()

Full name: pyslvs.get_include

return
str

Get include directory.

get_vlinks()

Full name: pyslvs.get_vlinks

vpoints	return
collections.abc.Iterable[VPoint]	list[VLink]

Get VLinks from a list of VPoint vpoints.

graph2vpoints()

Full name: pyslvs.graph2vpoints

graph	pos	cus	same	grounded	return
pyslvs.expression_parser.graph.Graph	dict[int, tuple[float, float]]	dict[int, int] | None	dict[int, int] | None	int | None	list[pyslvs.expression_parser.expression.VPoint]
		None	None	None

Transform graph into [VPoint] objects. The vertices are mapped to links.

• pos: Position for each vertices.
• cus: Extra points on the specific links.
• same: Multiple joint setting. The joints are according to edges_view.
• grounded: The ground link of vertices.

class LinkArgs

Full name: pyslvs.LinkArgs

Decorators
@dataclasses.dataclass(repr=False, eq=False)

Members	Type
color	str
name	str
points	str

Link table argument.

palp()

Full name: pyslvs.palp

c1	a0	d0	c2	inverse	return
pyslvs.tinycadlib.expression.Coord	float	float	pyslvs.tinycadlib.expression.Coord	bool	pyslvs.tinycadlib.expression.Coord
				False

The PALP function requires two points, one angle and one distance, obtained the position of fourth point.

In the following picture, c1 correspond to “A”, c2 correspond to “B”, d0 correspond to “L0”, a0 correspond to “alpha”, return correspond to “C”.

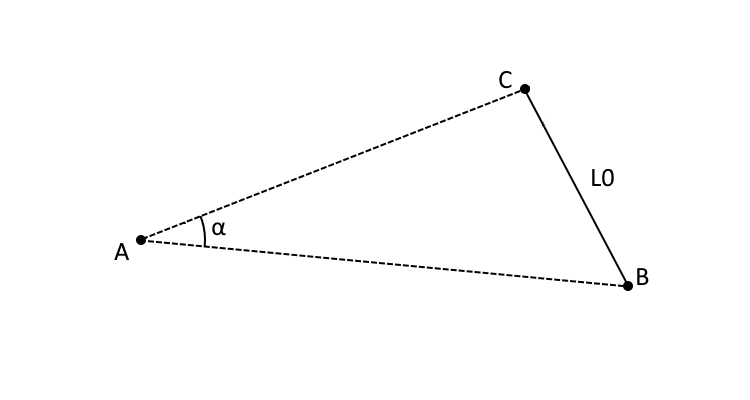
Set inverse option to True can make the result upside down.

parse_params()

Full name: pyslvs.parse_params

expr	return
str	list[PointArgs]

Parse mechanism expression into VPoint constructor arguments.

parse_pos()

Full name: pyslvs.parse_pos

expr	return
str	list[tuple[float, float]]

Parse mechanism expression into coordinates.

parse_vlinks()

Full name: pyslvs.parse_vlinks

expr	return
str	list[pyslvs.expression_parser.expression.VLink]

Parse mechanism expression into VLink objects.

parse_vpoints()

Full name: pyslvs.parse_vpoints

expr	return
str	list[pyslvs.expression_parser.expression.VPoint]

Parse mechanism expression into VPoint objects.

plap()

Full name: pyslvs.plap

c1	d0	a0	c2	inverse	return
pyslvs.tinycadlib.expression.Coord	float	float	pyslvs.tinycadlib.expression.Coord | None	bool	pyslvs.tinycadlib.expression.Coord
			None	False

The PLAP function requires two points, one distance and one angle, obtained the position of third point. The unit of a0 is degree.

In the following picture, c1 correspond to “A”, c2 correspond to “B”, d0 correspond to “L0”, a0 correspond to “beta”, return correspond to “C”. If c2 is not given, “alpha” will be set to zero.

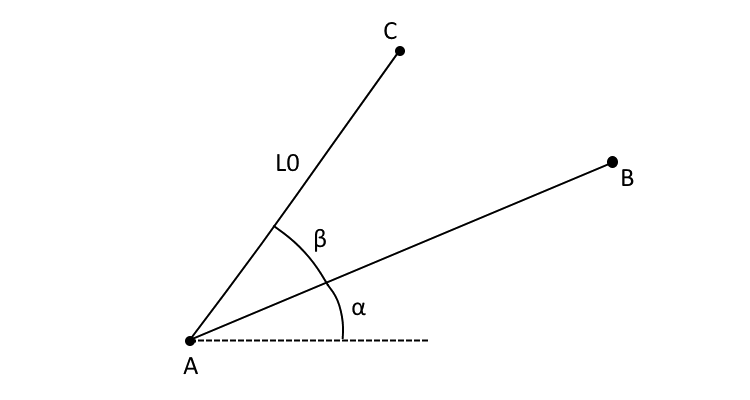
Set inverse option to True can make a0 value as negative.

pllp()

Full name: pyslvs.pllp

c1	d0	d1	c2	inverse	return
pyslvs.tinycadlib.expression.Coord	float	float	pyslvs.tinycadlib.expression.Coord	bool	pyslvs.tinycadlib.expression.Coord
				False

The PLLP function requires two points and two distances, obtained the position of third point.

In the following picture, c1 correspond to “A”, c2 correspond to “B”, d0 correspond to “L0”, d1 correspond to “L1”, return correspond to “C”.

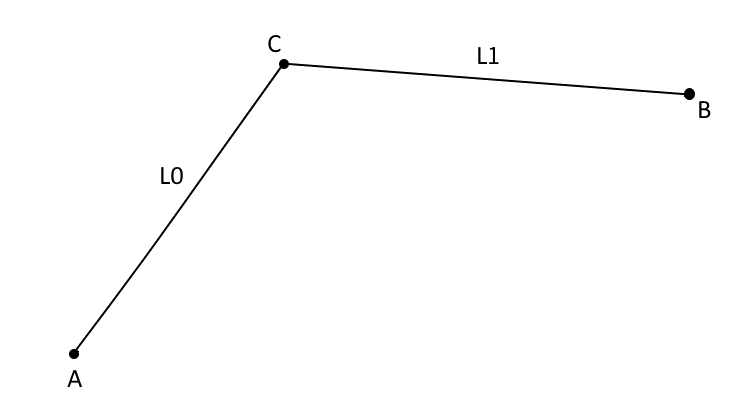
Set inverse option to True can make the result upside down.

plpp()

Full name: pyslvs.plpp

c1	d0	c2	c3	inverse	return
pyslvs.tinycadlib.expression.Coord	float	pyslvs.tinycadlib.expression.Coord	pyslvs.tinycadlib.expression.Coord	bool	pyslvs.tinycadlib.expression.Coord
				False

The PLPP function requires three points and one distance, obtained the position of fourth point.

In the following picture, c1 correspond to “A”, c2 correspond to “B”, c3 correspond to “C”, d0 correspond to “L0”, return correspond to “D”.

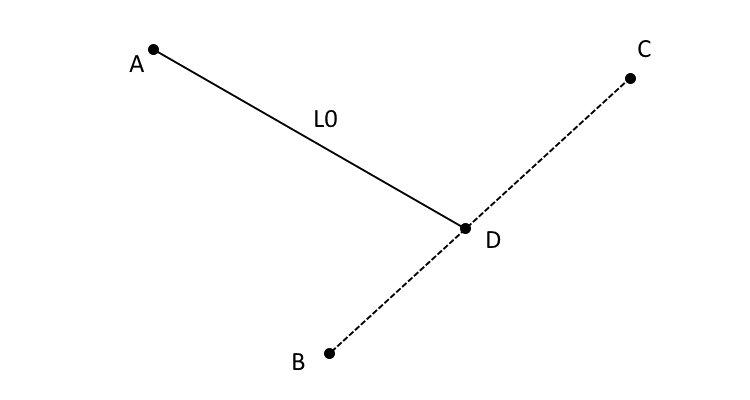
Set inverse option to True can make the result to the another side between c1 and line c2 c3.

class PointArgs

Full name: pyslvs.PointArgs

Decorators
@dataclasses.dataclass(repr=False, eq=False)

Members	Type
color	str
links	str
type	str
x	float
y	float

Point table argument.

ppp()

Full name: pyslvs.ppp

c1	c2	c3	return
pyslvs.tinycadlib.expression.Coord	pyslvs.tinycadlib.expression.Coord	pyslvs.tinycadlib.expression.Coord	pyslvs.tinycadlib.expression.Coord

The PPP function is used to solve parallel linkage.

In the following picture, c1 correspond to “A”, c2 correspond to “B”, c3 correspond to “C”, return correspond to “D”.

pxy()

Full name: pyslvs.pxy

c1	x	y	return
pyslvs.tinycadlib.expression.Coord	float	float	pyslvs.tinycadlib.expression.Coord

The PXY function requires one point and offset values, get the position of second point.

In the following picture, c1 correspond to “A”, d0 correspond to “X”, d1 correspond to “Y”, return correspond to “B”, the sign of value are correspond to coordinate system.

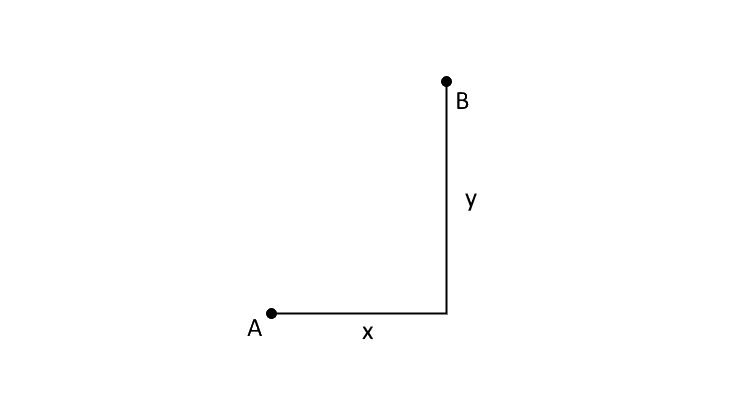
class SolverSystem

Full name: pyslvs.SolverSystem

Sketch Solve solver.

Note

The object attributes of such type are unable to access.

SolverSystem.__init__()

Full name: pyslvs.SolverSystem.__init__

self	vpoints	inputs	data_dict	return
Self	collections.abc.Sequence[pyslvs.bfgs.expression.VPoint]	collections.abc.Mapping[Tuple[int, int], float] | None	collections.abc.Mapping[_PointPair, Union[Coord, float]] | None	Any
		None	None

Initialize self. See help(type(self)) for accurate signature.

SolverSystem.same_points()

Full name: pyslvs.SolverSystem.same_points

self	vpoints_	return
Self	collections.abc.Sequence[pyslvs.bfgs.expression.VPoint]	bool

Return true if two expressions are same.

SolverSystem.set_data()

Full name: pyslvs.SolverSystem.set_data

self	data_dict	return
Self	collections.abc.Mapping[Tuple[int, int], float] | collections.abc.Mapping[int, Coord]	None

Set the values of data_dict parameter from original constructor. Two groups of dict keys must be the same or subset.

SolverSystem.set_inputs()

Full name: pyslvs.SolverSystem.set_inputs

self	inputs	return
Self	collections.abc.Mapping[tuple[int, int], float]	None

Set the values of inputs parameter from original constructor. Two groups of dict keys must be the same or subset.

SolverSystem.show_data()

Full name: pyslvs.SolverSystem.show_data

self	return
Self	frozenset[int | Tuple[int, int]]

Show the current keys of data_dict parameter from original constructor.

SolverSystem.show_inputs()

Full name: pyslvs.SolverSystem.show_inputs

self	return
Self	frozenset[tuple[int, int]]

Show the current input pairs keys from original constructor.

SolverSystem.solve()

Full name: pyslvs.SolverSystem.solve

self	return
Self	list[_Coord | Tuple[_Coord, _Coord]]

Solve the conditions and return the result, raise ValueError if not succeeded. The joint position will returned by its index correspondingly.

• Revolute joints: Tuple[float, float]
• Slider joints: Tuple[Tuple[float, float], Tuple[float, float]]

t_config()

Full name: pyslvs.t_config

vpoints	inputs	status	return
collections.abc.Sequence[pyslvs.topo_config.expression.VPoint]	collections.abc.Sequence[tuple[int, int]]	dict[int, bool] | None	EStack
		None

Generate the Triangle solution stack by mechanism expression vpoints_.

The argument inputs is a list of input pairs. The argument status will track the configuration of each point, which is optional.

uniform_expr()

Full name: pyslvs.uniform_expr

v	return
numpy.ndarray	list[pyslvs.tinycadlib.expression.VPoint]

Turn the uniform link length into expression.

uniform_four_bar()

Full name: pyslvs.uniform_four_bar

ml	n	return
float	int	numpy.ndarray

Generate n four bar mechanisms from maximum lengths.

These mechanisms have coupling points. Normalized parameters are $[L_0, L_2, L_3, L_4, \alpha]$.

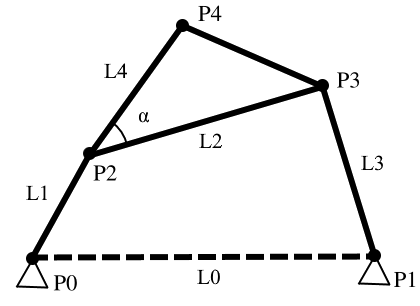
uniform_path()

Full name: pyslvs.uniform_path

v	n	return
numpy.ndarray	int	numpy.ndarray

Generate path with four-bar dimensions.

Normalized parameters are $[L_0, L_2, L_3, L_4, \alpha]$.

class VJoint

Full name: pyslvs.VJoint

Bases
enum.IntEnum

Enums
R
P
RP

An enumeration.

class VLink

Full name: pyslvs.VLink

Members	Type
FRAME	ClassVar[str]
HOLDER	ClassVar[VLink]
color	tuple[int, int, int] | None
color_str	str
name	str
points	collections.abc.Sequence[int]

Mechanism expression class in link’s view.

VLink.__contains__()

Full name: pyslvs.VLink.__contains__

self	point	return
Self	int	bool

Return key in self.

VLink.__init__()

Full name: pyslvs.VLink.__init__

self	name	color_str	points	color_func	return
Self	str	str	collections.abc.Iterable[int]	Callable[[str], _Color] | None	Any
				None

Initialize self. See help(type(self)) for accurate signature.

VLink.points_pos()

Full name: pyslvs.VLink.points_pos

self	vpoints	return
Self	collections.abc.Iterable[VPoint]	collections.abc.Sequence[Coord]

Get link positions from a VPoint list.

VLink.set_points()

Full name: pyslvs.VLink.set_points

self	points	return
Self	collections.abc.Iterable[int]	None

The update function of points attribute.

class VPoint

Full name: pyslvs.VPoint

Members	Type
HOLDER	ClassVar[VPoint]
angle	float
c	numpy.ndarray
color	tuple[int, int, int] | None
color_str	str
links	collections.abc.Sequence[str]
type	VJoint
type_str	str
x	float
y	float

Mechanism expression class.

VPoint.__getitem__()

Full name: pyslvs.VPoint.__getitem__

self	i	return
Self	int	float

Return self[key].

VPoint.__init__()

Full name: pyslvs.VPoint.__init__

self	links	type_int	angle	color_str	x	y	color_func	return
Self	collections.abc.Iterable[str]	VJoint	float	str	float	float	Callable[[str], _Color] | None	Any
							None

Initialize self. See help(type(self)) for accurate signature.

VPoint.copy()

Full name: pyslvs.VPoint.copy

self	return
Self	VPoint

The copy method of the VPoint object.

VPoint.cx()

Full name: pyslvs.VPoint.cx

Decorators
@property

self	return
Self	float

X value of current coordinate. If it’s slider, the pin coordinate will be returned.

VPoint.cy()

Full name: pyslvs.VPoint.cy

Decorators
@property

self	return
Self	float

Y value of current coordinate. If it’s slider, the pin coordinate will be returned.

VPoint.disable_offset()

Full name: pyslvs.VPoint.disable_offset

self	return
Self	None

Disable offset setting of the joint.

VPoint.distance()

Full name: pyslvs.VPoint.distance

self	p	return
Self	VPoint	float

Return the distance between two VPoint objects.

VPoint.expr()

Full name: pyslvs.VPoint.expr

self	return
Self	str

Return the literal mechanism expression of the joint.

VPoint.grounded()

Full name: pyslvs.VPoint.grounded

self	return
Self	bool

Return true if the joint pin is connected to ground link.

VPoint.has_offset()

Full name: pyslvs.VPoint.has_offset

self	return
Self	bool

Return true if the offset setting is enabled.

VPoint.is_slider()

Full name: pyslvs.VPoint.is_slider

self	return
Self	bool

Return true for slider type.

VPoint.is_slot_link()

Full name: pyslvs.VPoint.is_slot_link

self	link	return
Self	str	bool

Return true if the slot is on the link link_name.

VPoint.link_pos()

Full name: pyslvs.VPoint.link_pos

self	link	return
Self	str	Coord

Return the position for the vlink.

VPoint.locate()

Full name: pyslvs.VPoint.locate

self	x	y	return
Self	float	float	None

The update function of original coordinate.

VPoint.move()

Full name: pyslvs.VPoint.move

self	c1	c2	return
Self	tuple[float, float]	tuple[float, float] | None	None
		None

The update function of current coordinate(s). The 2^nd placement is the pin coordinate of slider joints.

If there is only one argument for a slider joint, the slot and pin coordinates will be set to the same position.

VPoint.no_link()

Full name: pyslvs.VPoint.no_link

self	return
Self	bool

Return true if there is no any link in links attribute.

VPoint.offset()

Full name: pyslvs.VPoint.offset

self	return
Self	float

Return the offset constraint value of the joint.

VPoint.pin_grounded()

Full name: pyslvs.VPoint.pin_grounded

self	return
Self	bool

Return true if the point is at the same link.

VPoint.r_joint()

Full name: pyslvs.VPoint.r_joint

Decorators
@staticmethod

links	x	y	return
collections.abc.Iterable[str]	float	float	VPoint

A fast constructor of revolute joints.

VPoint.replace_link()

Full name: pyslvs.VPoint.replace_link

self	link1	link2	return
Self	str	str	None

Replace the value in links attribute.

VPoint.rotate()

Full name: pyslvs.VPoint.rotate

self	angle	return
Self	float	None

The update function of angle attribute.

VPoint.same_link()

Full name: pyslvs.VPoint.same_link

self	p	return
Self	VPoint	bool

Return true if the point is at the same link.

VPoint.set_links()

Full name: pyslvs.VPoint.set_links

self	links	return
Self	collections.abc.Iterable[str]	None

The update function of links attribute.

VPoint.set_offset()

Full name: pyslvs.VPoint.set_offset

self	offset	return
Self	float	None

The update function of slider offset. It will also enable offset value after called.

VPoint.slider_joint()

Full name: pyslvs.VPoint.slider_joint

Decorators
@staticmethod

links	type_int	angle	x	y	return
collections.abc.Iterable[str]	VJoint	float	float	float	VPoint

A fast constructor of slider joints.

VPoint.slope_angle()

Full name: pyslvs.VPoint.slope_angle

self	p	num1	num2	return
Self	VPoint	int	int	float
		2	2

Return the value hypot(p_x - m_x, p_y - m_y), where m_x, m_y is the value of the joint, and p_x, p_y is the value of p.

The option num1 and num2 is the position of current coordinate attribute.

VPoint.sx()

Full name: pyslvs.VPoint.sx

Decorators
@property

self	return
Self	float

X value of slot coordinate.

VPoint.sy()

Full name: pyslvs.VPoint.sy

Decorators
@property

self	return
Self	float

Y value of slot coordinate.

VPoint.to_coord()

Full name: pyslvs.VPoint.to_coord

self	ind	return
Self	int	Coord

Obtain coordinate by Coord object.

VPoint.true_offset()

Full name: pyslvs.VPoint.true_offset

self	return
Self	float

Return the current offset value of the joint.

vpoint_dof()

Full name: pyslvs.vpoint_dof

vpoints	return
collections.abc.Sequence[pyslvs.tinycadlib.expression.VPoint]	int

Return the DOF of the mechanism expression vpoints.

Module pyslvs.efd

The source code refer from “spatial_efd” module.

calculate_efd()

Full name: pyslvs.efd.calculate_efd

contour	harmonic	return
numpy.ndarray	int	numpy.ndarray
	10

Compute the Elliptical Fourier Descriptors for a polygon.

Implements Kuhl and Giardina method of computing the coefficients An, Bn, Cn, Dn for a specified number of harmonics. This code is adapted from the pyefd module. See the original paper for more detail:

Kuhl, FP and Giardina, CR (1982). Elliptic Fourier features of a closed contour. Computer graphics and image processing, 18(3), 236-258.

Args: contour: A n x 2 numpy array represents a path. harmonic: The number of harmonics to compute for the given shape, defaults to 10. Returns: A numpy array of shape (harmonics, 4) representing the four coefficients for each harmonic computed.

fourier_power()

Full name: pyslvs.efd.fourier_power

coeffs	nyq	threshold	return
numpy.ndarray	int	float	int
		1.0

Compute the total Fourier power and find the minimum number of harmonics required to exceed the threshold fraction of the total power.

This is a good method for identifying the number of harmonics to use to describe a polygon. For more details see:

C. np_costa et al. / Postharvest Biology and Technology 54 (2009) 38-47

Warning: The number of coefficients must be >= the Nyquist Frequency. Args: coeffs: A numpy array of shape (n, 4) representing the four coefficients for each harmonic computed. nyq: The Nyquist Frequency. threshold: The threshold fraction of the total Fourier power, the default is 1. Returns: The number of harmonics required to represent the contour above the threshold Fourier power.

inverse_transform()

Full name: pyslvs.efd.inverse_transform

coeffs	locus_v	n	harmonic	return
numpy.ndarray	tuple[float, float]	int	int	numpy.ndarray

Perform an inverse fourier transform to convert the coefficients back into spatial coordinates.

Implements Kuhl and Giardina method of computing the performing the transform for a specified number of harmonics. This code is adapted from the pyefd module. See the original paper for more detail:

Kuhl, FP and Giardina, CR (1982). Elliptic Fourier features of a closed contour. Computer graphics and image procesnp_sing, 18(3), 236-258.

Args: coeffs: A numpy array of shape (n, 4) representing the four coefficients for each harmonic computed. locus_v: The x,y coordinates of the centroid of the contour being generated. Use calculate_dc_coefficients() to generate the correct locus for a shape. n: The number of coordinate pairs to compute. A larger value will result in a more complex shape at the expense of increased computational time. harmonic: The number of harmonics to be used to generate coordinates. Must be <= coeffs.shape[0]. Supply a smaller value to produce coordinates for a more generalized shape. Returns: A n x 2 numpy array represents a contour.

locus()

Full name: pyslvs.efd.locus

contour	return
numpy.ndarray	tuple[float, float]

Compute the dc coefficients, used as the locus when calling inverse_transform().

This code is adapted from the pyefd module. See the original paper for more detail:

Kuhl, FP and Giardina, CR (1982). Elliptic Fourier features of a closed contour. Computer graphics and image procesnp_sing, 18(3), 236-258.

Args: contour: A n x 2 numpy array represents a path. Returns: A tuple containing the c and d coefficients.

normalize_efd()

Full name: pyslvs.efd.normalize_efd

coeffs	norm	return
numpy.ndarray	bool	tuple[numpy.ndarray, float]
	True

Normalize the Elliptical Fourier Descriptor coefficients for a polygon.

Implements Kuhl and Giardina method of normalizing the coefficients An, Bn, Cn, Dn. Performs 3 separate normalizations. First, it makes the data location invariant by re-scaling the data to a common origin. Secondly, the data is rotated with respect to the major axis. Thirdly, the coefficients are normalized with regard to the absolute value of A_1. This code is adapted from the pyefd module. See the original paper for more detail:

Kuhl, FP and Giardina, CR (1982). Elliptic Fourier features of a closed contour. Computer graphics and image procesnp_sing, 18(3), 236-258.

Args: coeffs: A numpy array of shape (n, 4) representing the four coefficients for each harmonic computed. norm: Set to True (the default) to perform the third normalization and false to return the data withot this procesnp_sing step. Set this to False when plotting a comparison between the input data and the Fourier ellipse. Returns: A tuple consisting of a numpy.ndarray of shape (harmonics, 4) representing the four coefficients for each harmonic computed and the rotation in radians applied to the normalized contour.

rotate_contour()

Full name: pyslvs.efd.rotate_contour

contour	angle	centroid	return
numpy.ndarray	float	tuple[float, float]	numpy.ndarray

Rotates a contour about a point by a given amount expressed in degrees.

Operates by calling rotatePoint() on each x,y pair in turn. X and Y must have the same dimensions.

Args: contour: A n x 2 numpy array represents a path. angle: The angle in radians for the contour to be rotated by. centroid: A tuple containing the x,y coordinates of the centroid to rotate the contour about. Returns: A n x 2 numpy array represents a contour.

Module pyslvs.graph

Pyslvs graph functions.

contracted_graph()

Full name: pyslvs.graph.contracted_graph

link_num	stop_func	return
collections.abc.Sequence[int]	Callable[[], bool] | None	list[pyslvs.graph.structural.graph.Graph]
	None

Generate contracted graphs by link assortment link_num.

The check stop function stop_func object for GUI or subprocess, return True to terminate this function.

contracted_link_assortment()

Full name: pyslvs.graph.contracted_link_assortment

g	return
Graph	list[int]

Return contracted link assortment of the graph.

contracted_link_synthesis()

Full name: pyslvs.graph.contracted_link_synthesis

link_num_list	stop_func	return
collections.abc.Sequence[int]	Callable[[], bool] | None	list[tuple[int, ...]]
	None

Return contracted link assortment by link assortment link_num_list.

The check stop function stop_func object for GUI or subprocess, return True to terminate this function.

conventional_graph()

Full name: pyslvs.graph.conventional_graph

cg_list	c_j_list	no_degenerate	stop_func	return
list[pyslvs.graph.structural.graph.Graph]	collections.abc.Sequence[int]	int	Callable[[], bool] | None	list[pyslvs.graph.structural.graph.Graph]
		1	None

Generate conventional graphs by contracted graphs cg_list and contracted link assortment c_j_list.

The degenerate setting no_degenerate has following option:

• 0: No degenerate.
• 1: Only degenerate.
• Else: All graphs.

The check stop function stop_func object for GUI or subprocess, return True to terminate this function.

external_loop_layout()

Full name: pyslvs.graph.external_loop_layout

graph	node_mode	scale	return
pyslvs.graph.layout.graph.Graph	bool	float	dict[int, tuple[float, float]]
		1.0

Layout position decided by outer loop (max cycle).

Return the layout position decided by external loop. Argument node_mode will transform edges into vertices. Argument scale will resize the position by scale factor.

class Graph

Full name: pyslvs.graph.Graph

Members	Type
edges	tuple[tuple[int, int], ...]
vertices	tuple[int, ...]

The undirected graph class, support multigraph.

Graph.__init__()

Full name: pyslvs.graph.Graph.__init__

self	edges	return
Self	collections.abc.Iterable[tuple[int, int]]	Any

Initialize self. See help(type(self)) for accurate signature.

Graph.add_edge()

Full name: pyslvs.graph.Graph.add_edge

self	n1	n2	return
Self	int	int	None

Add edge n1 to n2.

Graph.add_vertices()

Full name: pyslvs.graph.Graph.add_vertices

self	vertices	return
Self	collections.abc.Iterable[int]	None

Add vertices from iterable object vertices.

Graph.adjacency_matrix()

Full name: pyslvs.graph.Graph.adjacency_matrix

self	return
Self	numpy.ndarray

Generate a adjacency matrix.

Assume the matrix $A[i, j] = A[j, i]$. Where $A[i, j] = 1$ if edge (i, j) exist.

Graph.copy()

Full name: pyslvs.graph.Graph.copy

self	return
Self	Graph

The copy method of the Graph object.

Graph.degree_code()

Full name: pyslvs.graph.Graph.degree_code

self	return
Self	int

Generate a degree code.

With a sorted vertices mapping by the degrees of each vertex, regenerate a new adjacency matrix. A binary code can be found by concatenating the upper right elements. The degree code is the maximum value of the permutation.

Graph.degrees()

Full name: pyslvs.graph.Graph.degrees

self	return
Self	dict[int, int]

Return the degrees of each vertex.

Graph.dof()

Full name: pyslvs.graph.Graph.dof

self	return
Self	int

Return DOF of the graph.

Note

DOF is the Degree of Freedoms to a mechanism.

In the [Graph] objects, all vertices will assumed as revolute joints (1 DOF).

$$F = 3(N_L - 1) - 2N_J$$

Graph.duplicate()

Full name: pyslvs.graph.Graph.duplicate

self	vertices	times	return
Self	collections.abc.Iterable[int]	int	Graph

Make graph duplicate by specific vertices. Return a new graph.

Graph.has_cut_link()

Full name: pyslvs.graph.Graph.has_cut_link

self	return
Self	bool

Return true if the graph has any cut links.

Graph.has_triangle()

Full name: pyslvs.graph.Graph.has_triangle

self	return
Self	bool

Return true if the graph has triangle.

Graph.is_connected()

Full name: pyslvs.graph.Graph.is_connected

self	without	return
Self	int	bool
	-1

Return True if the graph is connected. Set the argument without to ignore one vertex.

Graph.is_degenerate()

Full name: pyslvs.graph.Graph.is_degenerate

self	return
Self	bool

Return true if this kinematic chain is degenerate.

• Prue all multiple contracted links recursively.
• Check the DOF of sub-graph if it is lower then zero.

Graph.is_isomorphic()

Full name: pyslvs.graph.Graph.is_isomorphic

self	graph	return
Self	Graph	bool

Return true if two graphs is isomorphic.

Default is using VF2 algorithm.

Graph.is_isomorphic_degree_code()

Full name: pyslvs.graph.Graph.is_isomorphic_degree_code

self	graph	return
Self	Graph	bool

Compare isomorphism by degree code algorithm.

• https://doi.org/10.1115/1.2919236

Graph.is_isomorphic_vf2()

Full name: pyslvs.graph.Graph.is_isomorphic_vf2

self	graph	return
Self	Graph	bool

Compare isomorphism by VF2 algorithm, one of the high performance isomorphic algorithms.

Graph.neighbors()

Full name: pyslvs.graph.Graph.neighbors

self	n	return
Self	int	tuple[int, ...]

Return the neighbors of the vertex n.

is_planar()

Full name: pyslvs.graph.is_planar

g	return
pyslvs.graph.planar.graph.Graph	bool

Return true if the graph is a planar graph.

labeled_enumerate()

Full name: pyslvs.graph.labeled_enumerate

g	return
Graph	list[tuple[int, Graph]]

Enumerate each node with labeled except isomorphism.

link_assortment()

Full name: pyslvs.graph.link_assortment

g	return
Graph	list[int]

Return link assortment of the graph.

link_synthesis()

Full name: pyslvs.graph.link_synthesis

nl	nj	stop_func	return
int	int	Callable[[], bool] | None	list[tuple[int, ...]]
		None

Return link assortment by number of links nl and number of joints nj.

The check stop function stop_func object for GUI or subprocess, return True to terminate this function.

Module pyslvs.metaheuristics

Kernel of Metaheuristic Algorithm.

algorithm()

Full name: pyslvs.metaheuristics.algorithm

opt	return
AlgorithmType	type[pyslvs.metaheuristics.utility.Algorithm]

Return the class of the algorithms.

class Algorithm

Full name: pyslvs.metaheuristics.Algorithm

Bases
Generic[FVal]

Members	Type
func	ObjFunc[FVal]

Algorithm base class.

It is used to build the Meta-heuristic Algorithms.

Algorithm.__class_getitem__()

Full name: pyslvs.metaheuristics.Algorithm.__class_getitem__

cls	item	return
Self	Any	Any

Algorithm.__init__()

Full name: pyslvs.metaheuristics.Algorithm.__init__

Decorators
@abc.abstractmethod

self	func	settings	progress_fun	interrupt_fun	return
Self	ObjFunc[FVal]	pyslvs.metaheuristics.utility.config_types.Setting	Callable[[int, str], None] | None	Callable[[], bool] | None	Any
			None	None

Initialize self. See help(type(self)) for accurate signature.

Algorithm.history()

Full name: pyslvs.metaheuristics.Algorithm.history

self	return
Self	numpy.ndarray

Return the history of the process.

The first value is generation (iteration); the second value is fitness; the third value is time in second.

Algorithm.result()

Full name: pyslvs.metaheuristics.Algorithm.result

self	return
Self	tuple[numpy.ndarray, float]

Return the best variable vector and its fitness.

Algorithm.run()

Full name: pyslvs.metaheuristics.Algorithm.run

self	return
Self	FVal

Run and return the result and convergence history.

The first place of return is came from calling ObjFunc.result().

The second place of return is a list of generation data, which type is Tuple[int, float, float]]. The first of them is generation, the second is fitness, and the last one is time in second.

class AlgorithmType

Full name: pyslvs.metaheuristics.AlgorithmType

Decorators
@enum.unique

Bases
str
enum.Enum

Enums
RGA
DE
PSO
FA
TLBO

Enum type of algorithms.

class DE

Full name: pyslvs.metaheuristics.DE

Bases
pyslvs.metaheuristics.de.utility.Algorithm

The implementation of Differential Evolution.

DE.__init__()

Full name: pyslvs.metaheuristics.DE.__init__

self	func	settings	progress_fun	interrupt_fun	return
Self	pyslvs.metaheuristics.de.utility.ObjFunc[pyslvs.metaheuristics.de.utility.FVal]	pyslvs.metaheuristics.de.config_types.DESetting	Callable[[int, str], None] | None	Callable[[], bool] | None	Any
			None	None

Initialize self. See help(type(self)) for accurate signature.

default()

Full name: pyslvs.metaheuristics.default

opt	return
AlgorithmType	dict[str, int | float]

Return the default settings of the algorithms.

class DESetting

Full name: pyslvs.metaheuristics.DESetting

Bases
Setting

Members	Type
cr	float
f	float
strategy	pyslvs.metaheuristics.config_types.de.Strategy

class FA

Full name: pyslvs.metaheuristics.FA

Bases
pyslvs.metaheuristics.fa.utility.Algorithm

The implementation of Firefly Algorithm.

FA.__init__()

Full name: pyslvs.metaheuristics.FA.__init__

self	func	settings	progress_fun	interrupt_fun	return
Self	pyslvs.metaheuristics.fa.utility.ObjFunc[pyslvs.metaheuristics.fa.utility.FVal]	pyslvs.metaheuristics.fa.config_types.FASetting	Callable[[int, str], None] | None	Callable[[], bool] | None	Any
			None	None

Initialize self. See help(type(self)) for accurate signature.

class FASetting

Full name: pyslvs.metaheuristics.FASetting

Bases
Setting

Members	Type
alpha	float
beta0	float
beta_min	float
gamma	float

class ObjFunc

Full name: pyslvs.metaheuristics.ObjFunc

Bases
Generic[FVal]

Objective function base class.

It is used to build the objective function for Meta-heuristic Algorithms.

ObjFunc.fitness()

Full name: pyslvs.metaheuristics.ObjFunc.fitness

Decorators
@abc.abstractmethod

self	v	return
Self	numpy.ndarray	numpy.double

(cdef function) Return the fitness from the variable list v. This function will be directly called in the algorithms.

ObjFunc.result()

Full name: pyslvs.metaheuristics.ObjFunc.result

self	v	return
Self	numpy.ndarray	FVal

The result function. Default is the best variable vector v.

class PSO

Full name: pyslvs.metaheuristics.PSO

Bases
pyslvs.metaheuristics.pso.utility.Algorithm

Algorithm base class.

It is used to build the Meta-heuristic Algorithms.

PSO.__init__()

Full name: pyslvs.metaheuristics.PSO.__init__

self	func	settings	progress_fun	interrupt_fun	return
Self	pyslvs.metaheuristics.pso.utility.ObjFunc[pyslvs.metaheuristics.pso.utility.FVal]	pyslvs.metaheuristics.pso.config_types.PSOSetting	Callable[[int, str], None] | None	Callable[[], bool] | None	Any
			None	None

Initialize self. See help(type(self)) for accurate signature.

class RGA

Full name: pyslvs.metaheuristics.RGA

Bases
pyslvs.metaheuristics.rga.utility.Algorithm

The implementation of Real-coded Genetic Algorithm.

RGA.__init__()

Full name: pyslvs.metaheuristics.RGA.__init__

self	func	settings	progress_fun	interrupt_fun	return
Self	pyslvs.metaheuristics.rga.utility.ObjFunc[pyslvs.metaheuristics.rga.utility.FVal]	pyslvs.metaheuristics.rga.config_types.RGASetting	Callable[[int, str], None] | None	Callable[[], bool] | None	Any
			None	None

Initialize self. See help(type(self)) for accurate signature.

class RGASetting

Full name: pyslvs.metaheuristics.RGASetting

Bases
Setting

Members	Type
cross	float
delta	float
mutate	float
win	float

class Setting

Full name: pyslvs.metaheuristics.Setting

Bases
TypedDict

Members	Type
max_gen	int
max_time	float
min_fit	float
parallel	bool
pop_num	int
report	int
slow_down	float

class TLBO

Full name: pyslvs.metaheuristics.TLBO

Bases
pyslvs.metaheuristics.tlbo.utility.Algorithm

The implementation of Teaching Learning Based Optimization.

TLBO.__init__()

Full name: pyslvs.metaheuristics.TLBO.__init__

self	func	settings	progress_fun	interrupt_fun	return
Self	pyslvs.metaheuristics.tlbo.utility.ObjFunc[pyslvs.metaheuristics.tlbo.utility.FVal]	pyslvs.metaheuristics.tlbo.config_types.TOBLSetting	Callable[[int, str], None] | None	Callable[[], bool] | None	Any
			None	None

Initialize self. See help(type(self)) for accurate signature.

class TOBLSetting

Full name: pyslvs.metaheuristics.TOBLSetting

Bases
Setting

Module pyslvs.optimization

Pyslvs optimization targets.

cross_correlation()

Full name: pyslvs.optimization.cross_correlation

p1	p2	t	return
numpy.ndarray	numpy.ndarray	float	numpy.ndarray
		0.1

Compare signature and return as an 1d array.

$$\begin{aligned} C_n(j, W, P) &= \left|\sum_i^{l_P} \frac{(W_{i + j} - \overline{W}_{j\rightarrow j + l_P})(P_i-\overline{P})}{ \sqrt{\sum_i^{l_P}(W_{i + j} - \overline{W}_{j\rightarrow j + l_P})^2 \sum_i^{l_P}(P_i - \overline{P})^2}}\right| \\ S &= \arg\max\{C_n(j)\} t \end{aligned}$$

>>> from pyslvs.optimization import curvature, path_signature
>>> ps1 = path_signature(curvature(...))
>>> ps2 = path_signature(curvature(...))
>>> from pyslvs.optimization import cross_correlation
>>> cc = cross_correlation(ps1, ps2)

curvature()

Full name: pyslvs.optimization.curvature

path	return
collections.abc.Iterable[tuple[float, float]]	numpy.ndarray

Calculate the signed curvature and return as an array.

$$\kappa(t) = \frac{x'y'' - x''y'}{(x'^2 + y'^2)^\frac{3}{2}}$$

derivative()

Full name: pyslvs.optimization.derivative

path	return
numpy.ndarray	numpy.ndarray

Differential function. Return $p'$.

class FConfig

Full name: pyslvs.optimization.FConfig

Bases
TypedDict

Members	Type
expression	collections.abc.Sequence[pyslvs.expression.VPoint]
input	collections.abc.Sequence[tuple[Tuple[int, int], Sequence[float]]]
lower	float
placement	dict[int, tuple[float, float, float]]
same	dict[int, int]
shape_only	bool
target	dict[int, collections.abc.Sequence[Tuple[float, float]]]
upper	float

class FPlanar

Full name: pyslvs.optimization.FPlanar

Bases
pyslvs.metaheuristics.ObjFunc[str]

Members	Type
callback	int

A fast matching method that adds mapping angles to variables.

Allowing defects.

FPlanar.__init__()

Full name: pyslvs.optimization.FPlanar.__init__

self	mech	return
Self	pyslvs.optimization.f_planar.utility.FConfig	Any

Initialize self. See help(type(self)) for accurate signature.

FPlanar.fitness()

Full name: pyslvs.optimization.FPlanar.fitness

self	v	return
Self	numpy.ndarray	numpy.double

The fitness is the error between target path and self.

Chromosome format: (decided by upper and lower)

v: [Ax, Ay, Dx, Dy, ..., L0, L1, ..., A00, A01, ..., A10, A11, ...]

FPlanar.is_two_kernel()

Full name: pyslvs.optimization.FPlanar.is_two_kernel

self	return
Self	bool

Input a generic data (variable array), return the mechanism expression.

FPlanar.result()

Full name: pyslvs.optimization.FPlanar.result

self	v	return
Self	numpy.ndarray	str

Input a generic data (variable array), return the mechanism expression.

class NConfig

Full name: pyslvs.optimization.NConfig

Bases
TypedDict

Members	Type
target	collections.abc.Sequence[tuple[float, float]]

norm_path()

Full name: pyslvs.optimization.norm_path

path	scale	return
collections.abc.Iterable[tuple[float, float]]	float	numpy.ndarray
	1

Normalization function.

norm_pca()

Full name: pyslvs.optimization.norm_pca

path	return
collections.abc.Iterable[tuple[float, float]]	numpy.ndarray

Normalization function by PCA.

class NPlanar

Full name: pyslvs.optimization.NPlanar

Bases
pyslvs.metaheuristics.ObjFunc[str]

A normalized matching method.

Defects free. Normalized parameters are $[L_0, L_2, L_3, L_4, \alpha]$.

NPlanar.__init__()

Full name: pyslvs.optimization.NPlanar.__init__

self	mech	return
Self	pyslvs.optimization.n_planar.utility.NConfig	Any

Initialize self. See help(type(self)) for accurate signature.

NPlanar.fitness()

Full name: pyslvs.optimization.NPlanar.fitness

self	v	return
Self	numpy.ndarray	numpy.double

NPlanar.result()

Full name: pyslvs.optimization.NPlanar.result

self	v	return
Self	numpy.ndarray	str

path_signature()

Full name: pyslvs.optimization.path_signature

k	maximum	return
numpy.ndarray	float	numpy.ndarray
	100

Require a curvature, return path signature. It’s composed by curvature $\kappa$ and a $K$ value.

$$K = \int^t_0 |\kappa(t)| dt$$

>>> from pyslvs.optimization import curvature, path_signature
>>> path_signature(curvature(...))

Module pyslvs.metaheuristics.config_types

class PSOSetting

Full name: pyslvs.metaheuristics.config_types.PSOSetting

Bases
Setting

Members	Type
cognition	float
social	float
velocity	float

Module pyslvs.metaheuristics.de

class Strategy

Full name: pyslvs.metaheuristics.de.Strategy

Bases
enum.IntEnum

Enums
S1
S2
S3
S4
S5
S6
S7
S8
S9
S0

An enumeration.

Module pyslvs.metaheuristics.test

class TestObj

Full name: pyslvs.metaheuristics.test.TestObj

Bases
pyslvs.metaheuristics.test.utility.ObjFunc[float]

Test objective function.

f(x) = x1^2 + 8*x2

TestObj.fitness()

Full name: pyslvs.metaheuristics.test.TestObj.fitness

self	v	return
Self	numpy.ndarray	numpy.double

TestObj.result()

Full name: pyslvs.metaheuristics.test.TestObj.result

self	v	return
Self	numpy.ndarray	float

---

Last update: May 1, 2021